Laboratory works on geometries through Geogebra software

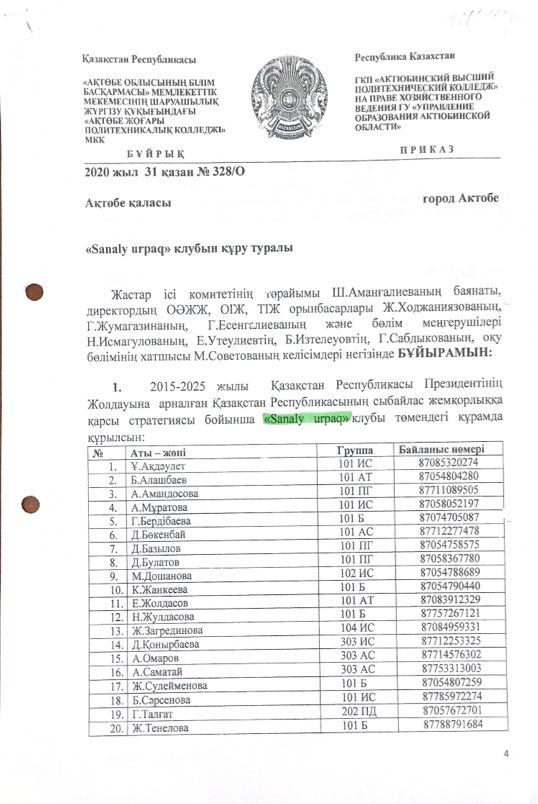
          Geometry is one of the levers to the development of spatial imagination, contributes to the formation of research and creative skills, therefore it has been and remains one of the most important school subjects. In the period of distance learning, instead of the usual tasks and drawings with a ruler and pencil, you can enter laboratory work through a dynamic environment. “Dynamic geometry is often called software environments that allow you to make geometric constructions on a computer in such a way that when the original objects move, the entire drawing is preserved.” The dynamic visual constructor provides students with the ability to creatively manipulate objects and, in general, a fully functional environment for designing and solving problems. One of the most convenient online geometry constructors is GeoGebra. The GeoGebra environment is free, allowing you to use it seamlessly wherever you are. It has a user-friendly interface. All graphic primitives are displayed on the toolbar. This tool allows you to create dynamic drawings. Dynamic drawings created in GeoGebra allow you to solve more problems in one lesson, consider all cases of solving a particular problem, prove a theorem, consider special cases, etc. Let’s look at an example that illustrates the use of the GeoGebra software tool. Example. Given circle S and point M outside it. Through point M are drawn all possible circles intersecting circle S. X is the point of intersection of the tangent at point M to the circle with the continuation of the common chord of circles S and. Find the locus of point X. Decision. Let A and B be the intersection points of the circles S and. Then, where O and R are, respectively, the center and radius of the circle S. Therefore, and hence, the point X lies on the perpendicular to the line OM. Step-by-step drawing creation in GeoGebra:

1. 1. 1. With the help of the tool “circle in the center and a point on it” draw a circle S with center O.
      2. We construct a circle with a center in the same way and in such a way that it intersects the circle S.
      3. Mark point A and point B at the intersection of the circles (tool “intersection” or “point”).
      4. Draw a tangent to the circle (the “tangent” tool), mark the tangency point M (the “point” tool).
      5. Using the two-point ray tool, draw a common chord.
      6. Mark the point of intersection of the chord and the tangent, point X (tool “intersection” or “point”).
      7. Select triangles AXM and OXB (tool “polygon”).
      8. Draw a straight line OM (the “two-point ray” tool).
      9. Drop the perpendicular from point X to OM (tool “perpendicular line”).
      As a result of the corresponding constructions in GeoGebra, we get the following figure (Fig. 1).