Геометрия является одним из рычагов к развитию пространственного воображения, способствует формированию исследовательских и творческих навыков, поэтому она была и остается одним из важнейших школьных предметов.
В период дистанционного обучения, вместо обычных заданий и чертежей линейкой с карандашом можно ввести лабораторные работы через динамическую среду.
«Динамической геометрией часто называют программные среды, которые позволяют делать геометрические построения на компьютере таким образом, что при движении исходных объектов весь чертёж сохраняется».
Динамический наглядный конструктор предоставляет студентам возможность творческой манипуляции с объектами и, в целом, полнофункциональную среду для конструирования и решения задач .
Одним из самых удобных онлайн конструкторов по геометрии является GeoGebra.
Среда GeoGebra распространяется бесплатно, что позволяет беспрепятственно использовать его везде, где вы находитесь. Она имеет удобный интерфейс. Все графические примитивы выведены на панель инструментов. Данный инструмент позволяет создавать динамические чертежи. Динамические чертежи, созданные в GeoGebra позволяют на одном уроке решить больше задач, рассмотреть все случаи решения той или иной задачи, доказательство теоремы, рассмотреть частные случаи и т. д .
Рассмотрим пример, иллюстрирующий применение средства программного обеспечения GeoGebra.
Пример.
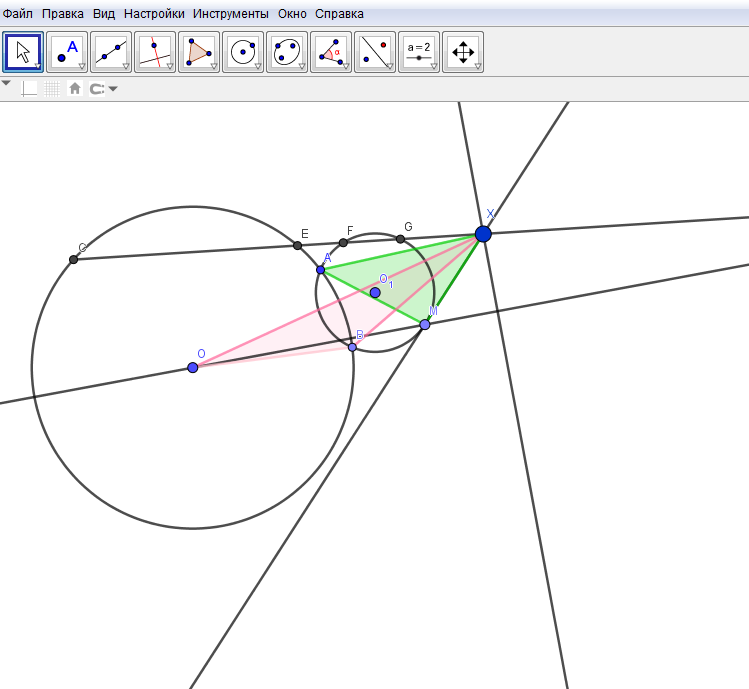
Дана окружность S и точка M вне ее. Через точку M проводятся все возможные окружности , пересекающие окружность S. X – точка пересечения касательной в точке M к окружности с продолжением общей хорды окружностей S и . Найдите геометрическое место точки Х .
Решение.
Пусть A и B – точки пересечения окружностей S и . Тогда, где O и R соответственно центр и радиус окружности S. Поэтому , а значит, точка X лежит на перпендикуляре к прямой OM.
Пошаговое создание чертежа в GeoGebra:
«Динамической геометрией часто называют программные среды, которые позволяют делать геометрические построения на компьютере таким образом, что при движении исходных объектов весь чертёж сохраняется».
Динамический наглядный конструктор предоставляет студентам возможность творческой манипуляции с объектами и, в целом, полнофункциональную среду для конструирования и решения задач .
Одним из самых удобных онлайн конструкторов по геометрии является GeoGebra.
Среда GeoGebra распространяется бесплатно, что позволяет беспрепятственно использовать его везде, где вы находитесь. Она имеет удобный интерфейс. Все графические примитивы выведены на панель инструментов. Данный инструмент позволяет создавать динамические чертежи. Динамические чертежи, созданные в GeoGebra позволяют на одном уроке решить больше задач, рассмотреть все случаи решения той или иной задачи, доказательство теоремы, рассмотреть частные случаи и т. д .
Рассмотрим пример, иллюстрирующий применение средства программного обеспечения GeoGebra.
Пример.
Дана окружность S и точка M вне ее. Через точку M проводятся все возможные окружности , пересекающие окружность S. X – точка пересечения касательной в точке M к окружности с продолжением общей хорды окружностей S и . Найдите геометрическое место точки Х .
Решение.
Пусть A и B – точки пересечения окружностей S и . Тогда, где O и R соответственно центр и радиус окружности S. Поэтому , а значит, точка X лежит на перпендикуляре к прямой OM.
Пошаговое создание чертежа в GeoGebra:
- С помощью инструмента «окружность по центру и точке на ней» строим окружность S с центром O.
- Окружность с центром , строим аналогично и таким образом, чтобы она пересекала окружность S.
- Отметим точку А и точку В на пересечении окружностей (инструмент «пересечение» или «точка»).
- Проведем касательную к окружности (инструмент «касательная»), отметим точку касания М (инструмент «точка»).
- С помощью инструмента «луч по двум точкам» проведем общую хорду.
- Отметим точку пересечения хорды и касательной, точка Х (инструмент «пересечение» или «точка»).
- Выделим треугольники АХМ и ОХВ (инструмент «многоугольник»).
- Проведем прямую ОМ (инструмент «луч по двум точкам»).
- Опустим перпендикуляр из точки Х на OM (инструмент «перпендикулярная прямая»).
В результате соответствующих построений в GeoGebra получаем следующий рисунок (рис. 1).
Рис.1. Чертеж к примеру 1.
На средах динамической геометрии можно рассматривать не только задачи, но и теоремы.
Таким образом, интерактивную геометрическую среду GeoGebra можно рассматривать как удобный программный продукт, который может эффективно применяться для обучения геометрии или проведений лабораторных работ. Использование этой программы не требует длительного обучения и не навредит учебному процессу, а наоборот, повысит интерес и мотивацию учащихся к изучению предмета.
Таким образом, интерактивную геометрическую среду GeoGebra можно рассматривать как удобный программный продукт, который может эффективно применяться для обучения геометрии или проведений лабораторных работ. Использование этой программы не требует длительного обучения и не навредит учебному процессу, а наоборот, повысит интерес и мотивацию учащихся к изучению предмета.